Op-Amp Sebagai Integrator
Op-Amp sebagai penguat dapat difungsikan untuk melakukan operasi
matematik seperti integrasi dan differensiasi terhadap sinyal masukan yang
diberikan. Integrator merupakan konfigurasi Op-Amp yang berfungsi untuk
menguatkan hasil integrasi dari sinyal masukan yang diberikan. Misalnya jika
sinyal masukan dari integrator berbentuk gelombang sinus maka akan
menghasilkan sinyal keluaran berupa gelombang negatif cosinus. Dengan
fungsi tersebut, integrator sering digunakan untuk mengubah bentuk sinyal.
Beberapa bentuk sinyal yang dapat diubah oleh integrator yaitu gelombang
persegi menjadi segitiga, gelombang sinus menjadi negatif cosinus, dan
gelombang segitiga menjadi sinus. Integrator sering disebut dengan penguat
integrasi. Rangkaian dari integrator pada dasarnya berupa penguat inverting yang resistor umpan bailknya diganti dengan komponen kapasitor. Gambar 1.
menunjukan rangkaian integrator.
 |
| Gambar 1. Op-Amp Sebagai Integrator |
Analisis Rangkaian Integrator
Dalam menganalisis rangkaian Op-Amp sebagai penguat terdapat dua
aturan penting yang perlu diperhatikan. Kedua aturan tersebut menggunakan
karakteristik Op-Amp ideal. Aturan ini dalam beberapa literatur dinamakan
golden rule, yang berisi :
- Perbedaan tegangan antara kedua masukan Op-Amp adalah nol (V+ - V- = 0 atau V+ = V-), hal ini bertujuan menghindari adanya tegangan offset. Aturan pertama ini sering disebut dengan virtual ground.
- Arus yang mengalir pada kedua masukan Op-Amp adalah nol (I+ = I- = 0), hal ini dikarenakan impedansi input pada Op-Amp sangat besar ( Zin = ∞). Dengan memahami kedua aturan tersebut, analisis dari rangkaian Op-Amp akan menjadi lebih mudah.
Untuk memulai analisis rangkaian integrator, terapkan hukum Kirchoff
arus pada titik cabang A dan asumsi I+ = I- = 0, sehingga gambar rangkaian
integrato menjadi seperti Gambar 2.
 |
| Gambar 2. Analisis Rangkaian Integrator |
Karena rangkaian integrator menggunakan komponen kapasitor, maka perlu
diketahui terlebih dahulu hubungan arus dan tegangan dari kapasitor yaitu:
Persamaan (1)
Dari Gambar 2. didapatkan persamaan arus yang mengalir pada titik cabang
A, sebagai berikut:
Persamaan (2)
Dengan menggunakan teori tegangan titik simpul, dan menerapkan persamaan
arus kapasitor Ic pada arus umpan balik If maka persamaan (2) dapat
dijabarkan menjadi:
Persamaan (3)
Karena V+ = 0 dan V- = VA , serta asumsi nilai V+ = V- maka dapat dituliskan
nilai VA = 0. Sehingga persamaan (3) menjadi:
Persamaan (4)
Dengan melakukan integrasi pada kedua sisi dari persamaan (4), dapat
diperoleh persamaan tegangan keluaran dari integrator:
Persamaan (5)
Dimana K merupakan konstanta integrasi terhadap waktu yang nilainya sesuai
dengan nilai tegangan keluaran (Vout) saat t = 0 detik.
Untuk mencari persamaan penguatan dari rangkaian integrator dapat dilakukan
menggunakan persamaan penguatan penguat inverting, karena konfigurasi
rangkaian integrator mirip dengan konfigurasi penguat inverting. hanya saja
hambatan Rf diganti dengan reaktansi kapasitif (XC) dari kapasitor Cf.
Persamaan (6)
Dimana nilai dari XC sendiri, didapatkan dari:
Persamaan (7)
Keterangan:
𝑋𝐶 = reaktansi kapasitif (Ω)
𝜔 = 2𝜋𝑓 = frekuensi radian (rad/s)
𝜋 = 3,14
𝑓 = frekuensi (Hz)
𝐶𝑓 = Kapasitor umpan balik (F)
Dengan mensubtitusikan persamaan (7) ke dalam persamaan (6), dapat
diperoleh persamaan penguatan dari integrator:
Persamaan (8)
Karena 𝜔 nilainya sama dengan 2𝜋𝑓, penguatan integrator pada persamaan
(8) menjadi:
Persamaan (9)
Keterangan:
AV = penguatan tegangan
Vin = tegangan masukan
Vout = Tegangan Keluaran
Dari persamaan (9) dapat diketahui bahwa nilai penguatan integrator
berbanding terbalik dengan frekuensi, semakin besar nilai frekuensi akan
membuat nilai penguatan semakin kecil dan sebaliknya. Hal ini menyebabkan
rangkaian integrator sering digunakan sebagai low pass filter, yaitu filter yang
meloloskan sinyal dengan frekuensi rendah dan meredam sinyal dengan
frekuensi tinggi.
Contoh Soal
Contoh 1:
Integrator memiliki nilai R1 = 100 kΩ, dan Cf = 1 uF. Tentukan berapa nilai
tegangan keluar dari integrator tersebut jika diberi tegangan masukan berupa
gelombang sinus dengan nilai 2 sin 4t V!
Jawab :
Untuk menghitung nilai tegangan keluaran dari integrator dapat dilakukan
menggunakan persamaan (5):
Contoh 2:
Integrator memiliki nilai R1 = 200 Ω, dan Cf = 10 uF. Tentukan berapa nilai
penguatan dari integrator tersebut jika diberi sinyal masukan dengan frekuensi
50 Hz!
Jawab :
Untuk menghitung nilai penguatan dari integrator dapat dilakukan
menggunakan persamaan (9):









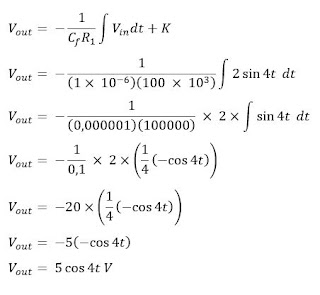


Bagus bang ilmu nya tapi banyak typo pass cintoh soal nya
BalasHapus